Часть Перемещение
12.2.1.1. Часть 1: Перемещение
Чтобы точка p совпадала с началом координат, ее необходимо переместить на –p, поскольку p– p = 0. Так что отвечающая за перемещение часть матрицы преобразования вида задается следующей матрицей:
Построение гибкого класса камеры
До сих пор для вычисления матрицы преобразования пространства вида мы пользовались функцией D3DXMatrixLookAtLH. Она вполне подходит для размещения и нацеливания неподвижной камеры, но пользовательский интерфейс часто требует, чтобы камера перемещалась в ответ на действия пользователя. Поэтому нам необходимо разработать собственное решение. В данной главе мы посмотрим как реализовать класс Camera, предоставляющий большую свободу управления камерой, чем функция D3DXMatrixLookAtLH, и подходящий для авиасимуляторов и игр с видом от первого лица.
| Цели | |
|
Изучить реализацию гибкого класса Camera, который может использоваться в авиасимуляторах и играх с видом от первого лица. |
Ходьба, сдвиг и полет
12.2.4. Ходьба, сдвиг и полет
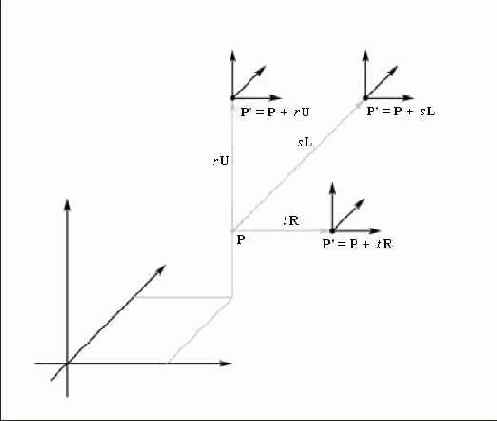
Говоря о ходьбе мы подразумеваем перемещение в направлении взгляда (то есть вдоль вектора взгляда). Сдвиг— это перемещение в сторону относительно направления взгляда, то есть перемещение вдоль правого вектора. Ну и когда мы говорим о полете, подраумевается перемещение вдоль верхнего вектора. Чтобы переместиться вдоль одной из этих осей мы просто прибавляем к вектору местоположения камеры вектор заданной длины, указывающий в том же направлении, что и ось, вдоль которой перемещается камера (Рисунок 12.7).
с помощью четырех векторов: правогоМы описываем местоположение и ориентацию камеры в мировой системе координат с помощью четырех векторов: правого вектора, верхнего вектора, вектора взгляда и вектора местоположения. Такое описание позволяет легко реализовать камеру с шестью степенями свободы, предоставляющую гибкий интерфейс подходящий для авиационных симуляторов и для игр с видом от первого лица. Наклон, или поворот относительно правого вектора камеры
 |
|||
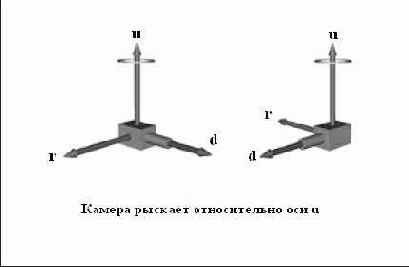
Наклон, рыскание и вращение
Поскольку векторы ориентации описывают ориентацию камеры относительно мировой системы координат, мы должны вычислять как они изменяются при наклоне, рыскании и вращении камеры. Сделать это очень просто. Взгляните на Рисунок 12.4, 12.5 и 12.6, где изображен наклон, рыскание и вращение камеры соответственно.
Как и в случае с поворотами камеры, для наземных объектов мы вносим ряд ограничений. К примеру, объекты LANDOBJECT не могут находиться в воздухе, даже если верхний вектор изменяется в результате движения вперед или сдвига вбок. Следовательно, мы должны ограничить их перемещение плоскостью XZ. Но, поскольку наземные объекты могут изменять свою высоту, взбираясь на лестницы или холмы, мы предоставляем метод Camera::setPosition, позволяющий вручную разместить камеру в требуемом месте и на требуемой высоте. Код реализации ходьбы, сдвига и полета выглядит следующим образом: void Camera::walk(float units) { // Для наземных объектов перемещение только в плоскости xz if(_cameraType == LANDOBJECT) _pos += D3DXVECTOR3(_look.x, 0.0f, _look.z) * units; if(_cameraType == AIRCRAFT) _pos += _look * units; } void Camera::strafe(float units) { // Для наземных объектов перемещение только в плоскости xz if(_cameraType == LANDOBJECT) _pos += D3DXVECTOR3(_right.x, 0.0f, _right.z) * units; if(_cameraType == AIRCRAFT) _pos += _right * units; } void Camera::fly(float units) { if(_cameraType == AIRCRAFT) _pos += _up * units; } Преобразование из мирового пространства
 Следовательно, нам нужна матрица преобразования V, отвечающая следующим требованиям: pV = (0, 0, 0) — Матрица преобразования V перемещает камеру в начало координат. rV = (1, 0, 0) — Матрица V преобразует правый вектор камеры таким образом, чтобы он совпадал с осью X мировой системы координат. uV = (0, 1, 0) — Матрица V преобразует верхний вектор камеры таким образом, чтобы он совпадал с осью Y мировой системы координат. dV = (0, 0, 1) — Матрица V преобразует вектор взгляда камеры таким образом, чтобы он совпадал с осью Z мировой системы координат. Задачу нахождения такой матрицы можно разделить на две части: 1) перемещение, в результате которого камера окажется в начале системы координат и 2) поворот, в результате которого оси камеры будут совпадать с осями мировой системы координат. Пример приложения: камераПример приложния к данной главе создает и визуализрует сцену, изображенную на Рисунок 12.8. Проектирование класса камерыМы определяем местоположение и ориентацию камеры относительно мировой системы координат с помощью четырех векторов камеры (camera vectors): правого вектора (right vector), верхнего вектора (up vector), вектора взгляда (look vector) и вектора местоположения (position vector), как показано на Рисунок 12.1. Эти векторы образуют локальную систему координат камеры, описанную в мировой системе координат. Поскольку правый вектор, верхний вектор и вектор взгляда описывают ориентацию камеры в мировом пространстве, мы иногда будем называть их векторами ориентации (orientation vectors). Векторы ориентации должны быть ортонормальными. Набор векторов называется ортонормальным, если каждый вектор перпендикулярен остальным и длина всех векторов равна единице. Причина данного ограничения в том, что позже мы подставим эти векторы в строки матрицы, а матрица в которой векторы-строки являются ортонормальными будет ортогональной. Вспомните, что отличительной особенностью ортогональной матрицы является то, что результат ее транспонирования равен результату ее инвертирования. Пользу этой особенности мы увидим в разделе 12.2.1.2.
Эти четыре описывающих камеру вектора позволяют выполнять с камерой следующие шесть операций: Поворот относительно правого вектора (наклон). Поворот относительно верхнего вектора (отклонение). Поворот относительно вектора взгляда (вращение). Сдвиг вдоль правого вектора. Подъем вдоль верхнего вектора. Передвижение вдоль вектора взгляда. Эти шесть операций позволяют нам перемещать камеру вдоль трех осей и вращать ее вокруг этих же осей, что дает в совокупности шесть степеней свободы. Приведенное ниже определение класса Camera отражает наше описание данных и требуемые методы: class Camera { public: enum CameraType { LANDOBJECT, AIRCRAFT }; Camera(); Camera(CameraType cameraType); ~Camera(); void strafe(float units); // влево/вправо void fly(float units); // вверх/вниз void walk(float units); // вперед/назад void pitch(float angle); // вращение относительно правого вектора void yaw(float angle); // вращение относительно верхнего вектора void roll(float angle); // вращение относительно вектора взгляда void getViewMatrix(D3DXMATRIX* V); void setCameraType(CameraType cameraType); void getPosition(D3DXVECTOR3* pos); void setPosition(D3DXVECTOR3* pos); void getRight(D3DXVECTOR3* right); void getUp(D3DXVECTOR3* up); void getLook(D3DXVECTOR3* look); private: CameraType _cameraType; D3DXVECTOR3 _right; D3DXVECTOR3 _up; D3DXVECTOR3 _look; D3DXVECTOR3 _pos; }; В этом определении класса есть одна вещь, которую мы до сих пор не обсуждали — перечисление CameraType. Дело в том, что наша камера поддерживает две модели поведения: LANDOBJECT и AIRCRAFT. Модель AIRCRAFT позволяет свободно перемещаться в пространстве и предоставляет шесть степеней свободы. В то же время в ряде игр с видом от первого лица персонаж не может летать, и нам надо ограничить перемещение по соответствующей оси. Чтобы внести эти ограничения, достаточно указать для камеры тип LANDOBJECT, что будет показано в последующих разделах. Вращение, или поворот относительно вектора взгляда камеры
 |
Как видите при наклоне камеры мы должны повернуть верхний вектор и вектор взгляда относительно правого вектора на заданный угол. Аналогично при рыскании мы поворачиваем правый вектор и вектор взгляда относительно верхнего вектора на указанный угол. А при вращении камеры мы поворачиваем на заданный угол верхний и правый векторы относительно вектора взгляда.
Теперь вы видите, почему нам необходима функция D3DXMatrixRotationAxis, ведь любой из трех векторов относительно которых выполняется поворот, в мировой системе координат может иметь произвольную ориентацию.
Реализация методов для наклона, рыскания и вращения соответствует приведенному выше описанию. Однако для типа камеры LANDOBJECT добавлен ряд ограничений. В частности, неестественно выглядит отклонение от заданного курса при наклоне или вращении наземного объекта. Поэтому при рыскании в модели LANDOBJECT мы выполняем поворот относительно оси Y мировой системы координат, а не относительно верхнего вектора камеры. Кроме того, мы полностью запрещаем вращение наземных объектов. Помните об этом, когда будете использовать класс Camera в своих собственных приложениях; мы предлагаем вам только пример.
Код реализующий наклон, рыскание и вращение камеры выглядит так:
void Camera::pitch(float angle) { D3DXMATRIX T; D3DXMatrixRotationAxis(&T, &_right, angle);
// Поворот векторов _up и _look относительно вектора _right D3DXVec3TransformCoord(&_up,&_up, &T); D3DXVec3TransformCoord(&_look,&_look, &T); }
void Camera::yaw(float angle) { D3DXMATRIX T;
// Для наземных объектов выполняем вращение // вокруг мировой оси Y (0, 1, 0) if(_cameraType == LANDOBJECT) D3DXMatrixRotationY(&T, angle);
// Для летающих объектов выполняем вращение // относительно верхнего вектора if(_cameraType == AIRCRAFT) D3DXMatrixRotationAxis(&T, &_up, angle);
// Поворот векторов _right и _look относительно // вектора _up или оси Y D3DXVec3TransformCoord(&_right, &_right, &T); D3DXVec3TransformCoord(&_look, &_look, &T); }
void Camera::roll(float angle) { // Вращение только для летающих объектов if(_cameraType == AIRCRAFT) { D3DXMATRIX T; D3DXMatrixRotationAxis(&T, &_look, angle);
// Поворот векторов _up и _right относительно // вектора _look D3DXVec3TransformCoord(&_right, &_right, &T); D3DXVec3TransformCoord(&_up, &_up, &T); } }
Вращение относительно произвольной оси, определенной вектором A
Рисунок 12.3. Вращение относительно произвольной оси, определенной вектором A
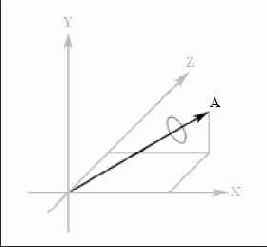
Предположим, мы хотим выполнить поворот на π/2 радиан вокруг оси, заданной вектором (0.707,0.707, 0). Для этого надо написать:
D3DXMATRIX R; D3DXVECTOR3 axis(0.707f, 0.707f, 0.0f); D3DXMatrixRotationAxis(&R, &axis, D3DX_PI / 2.0f);
Формулу, по которой функция D3DXMatrixRotationAxis вычисляет матрицу вращения вы найдете в книге Эрика Ленджела «Mathematics for 3D Game Programming & Computer Graphics».
12.2.2. Вращение относительно произвольной оси
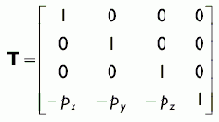
Чтобы реализовать методы для поворота нашей камеры, нам необходима возможность вращать ее относительно произвольной оси. Для этой цели библиотека D3DX предоставляет следующую функцию:
D3DXMATRIX *D3DXMatrixRotationAxis( D3DXMATRIX *pOut, // возвращает матрицу вращения CONST D3DXVECTOR3 *pV, // ось вращения FLOAT Angle // угол поворота в радианах );
Вычисление матрицы вида
Сейчас мы покажем, как можно вычислить матрицу преобразования вида, на основании заданных векторов камеры. Предположим, что векторы p= (px, py, pz), r = (rx, ry, rz), u = (ux, uy, uz) и d = (dx, dy, dz) являются соответственно вектором местоположения, правым вектором, верхним вектором и вектором взгляда камеры. Вспомните, что в главе 2 мы говорили о том, что преобразование пространства вида трансформирует геометрию мира таким образом, что камера помещается в начало координат и ее оси совпадают с осями мировой системы координат (Рисунок 12.2). 
|