A) Луч проходит мимо сферы; и
Рисунок 15.4. a) Луч проходит мимо сферы; и t0 и t1 мнимые числа б) Луч находится за сферой; и t0 и t1 отрицательные числа. в) Луч начинается внутри сферы; одно из решений положительное, а другое — отрицательное. Положительное решение соответствует единственной точке пересечения. г) Луч пересекает сферу; и t0 и t1 положительные числа. д) Луч касается сферы в единственной точке; в этом случае оба решения положительны и t0 = t1.
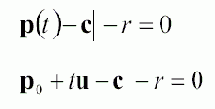
Приведенный ниже метод возвращает true, если переданный в первом параметре луч пересекает переданную во втором параметре сферу. Если луч проходит мимо сферы, метод возвращает false:
bool PickApp::raySphereIntersectionTest(Ray* ray, BoundingSphere* sphere) { D3DXVECTOR3 v = ray->_origin - sphere->_center;
float b = 2.0f * D3DXVec3Dot(&ray->_direction, &v); float c = D3DXVec3Dot(&v, &v) – (sphere->_radius * sphere->_radius);
// Находим дискриминант float discriminant = (b * b) - (4.0f * c);
// Проверяем на мнимые числа if(discriminant < 0.0f) return false;
discriminant = sqrtf(discriminant);
float s0 = (-b + discriminant) / 2.0f; float s1 = (-b - discriminant) / 2.0f;
// Если есть решение >= 0, луч пересекает сферу if(s0 >= 0.0f || s1 >= 0.0f) return true;
return false; }
Конечно, мы уже показывали объявление структуры BoundingSphere, но для удобства приведем его здесь еще раз:
struct BoundingSphere { BoundingSphere();
D3DXVECTOR3 _center; float _radius; };
Длина вектора p – c, обозначаемая
Рисунок 15.3. Длина вектора p – c, обозначаемая как |p – c|, равна радиусу сферы, если точка p лежит на поверхности сферы. Обратите внимание, что на иллюстрации для простоты изображен круг, но идея работает и в трех измерениях

Чтобы определить, пересекает ли луч p(t) = p0 + tu сферу и, если да, то где, мы подставляем формулу луча в уравнение сферы и ищем значение параметра t, удовлетворяющее уравнению сферы, что позволит нам найти точки пересечения.
Подставляем формулу луча в уравнение сферы:
Выбор объектов
Предположим, что пользователь щелкает по точке экрана s= (x, y). На Рисунок 15.1 видно, что в этом случае пользователь выбрал чайник. Однако приложение не может немедленно определить, что при щелчке по точке s выбран именно чайник. Существует техника, позволяющая определить, какой именно из объектов сцены выбран. Эта техника называется выбором объектов (picking).
это техника используемая для определения
Выбор объекта — это техника используемая для определения трехмерного объекта, соответствующего отображаемой на экране двухмерной проекции по которой щелкнул пользователь.
Луч выбора формируется путем создания луча, начинающегося в начале координат пространства вида и проходящего через точку окна проекции, соответствующую той точке экрана, по которой щелкнул пользователь.
Мы можем преобразовать луч r(t) = p0 + tu преобразовав по отдельности его начальную точку p0 и вектор направления u с помощью матрицы преобразования. Обратите внимание, что начало луча преобразуется как точка (w = 1), а направление — как вектор (w = 0).
Чтобы проверить, пересекает ли луч объект, мы можем проверить пересекает ли луч какую-нибудь из треугольных граней объекта или проверить пересекает ли луч ограничивающий объем объекта, например, ограничивающую сферу.
Луч, проходящий через точку p
Рисунок 15.2. Луч, проходящий через точку p, пересекает объект, если точка p находится внутри его проекции. Обратите внимание, что точка p в окне проекции соответствует точке s на экране, по которой щелкнул пользователь
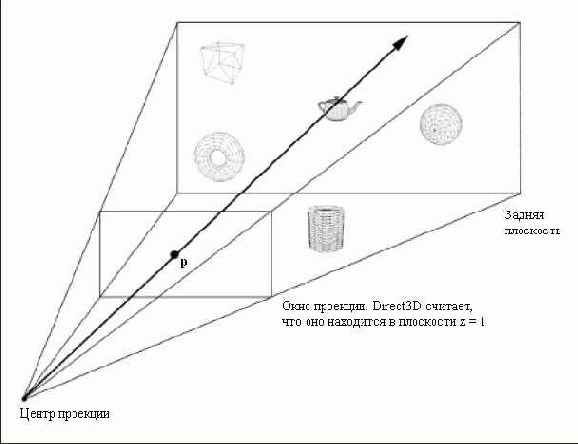
На Рисунок 15.2 видно, что луч, начинающийся в начале координат и проходящий через точку p пересекает тот объект, внутри которого находится точка p, в нашем случае это чайник. Следовательно, вычислив луч выбора мы можем перебрать все объекты сцены и проверить, пересекает ли их луч. Тот объект, который пересекает луч, и будет тем объектом, который выбрал пользователь. Ну и снова скажем, что в нашем примере это чайник.
Итак, в примере у нас есть точка s и чайник. В общем случае у нас есть точка экрана по которой щелкнул пользователь. Теперь нам надо вычислить луч выбора и проверить все объекты сцены, не пересекает ли их этот луч. Тот объект, который пересекает луч и будет тем объектом, который выбрал пользователь. Может случиться так, что луч не пересекает никаких объектов. Например, на Рисунок 15.1 пользователь может не выбирать один из четырех объектов на экране, а щелкнуть по белому фону, и луч выбора не пересечет ни один из объектов. Таким образом мы можем заключить, что если луч не пересекает ни один из объектов сцены, значит пользователь выбрал фон или что-нибудь не представляющее для нас интереса.
Выбор объектов используется во всех играх и трехмерных приложениях. Например, почти всегда пользователь взаимодействует с объектами игрового мира щелкая по их изображениям мышью. Игрок может щелкнуть по врагу, чтобы выстрелить в него, или по предмету, чтобы взять его. Чтобы игра правильно реагировала на действия пользователя, нам надо определить по какому объекту произведен щелчок (это враг или предмет?) и местоположение этого объекта в пространстве (куда должен быть выпущен снаряд или может ли игрок дотянуться до этого предмета?). На все эти вопросы и дает ответ выбор объектов.
| Цели | |
|
Изучить реализацию алгоритма выбора объектов и понять как он работает. Выбор объектов можно разделить на четыре этапа: Получение данных точки экрана s по которой был сделан щелчок и вычисление соответствующей ей точки p в окне проекции. Вычисление луча выбора, который начинается в начале координат и проходит через точку p. Преобразование луча выбора и объектов сцены в одну общую систему координат. Определение объекта, пересекаемого лучом выбора. Тот объект, который пересекает луч, и есть тот объект, который выбрал пользователь на экране. |
Окно примера к данной главе
Рисунок 15.5. Окно примера к данной главе

На Рисунок 15.5 показано окно приложения, созданного для данной главы. Чайник перемещается по экрану, а вы должны попытаться щелкнуть по нему мышкой. Если вы попали в ограничивающую сферу чайника, на экран будет выведено сообщающее об этом диалоговое окно. Мы обрабатываем событие щелчка кнопки мыши проверяя сообщение WM_LBUTTONDOWN:
case WM_LBUTTONDOWN: // Вычисляем луч в пространстве вида на основании // координат указателя мыши в момент щелчка d3d::Ray ray = CalcPickingRay(LOWORD(lParam), HIWORD(lParam));
// Преобразуем луч в мировое пространство D3DXMATRIX view; Device->GetTransform(D3DTS_VIEW, &view);
D3DXMATRIX viewInverse; D3DXMatrixInverse(&viewInverse, 0, &view);
TransformRay(&ray, &viewInverse);
// Проверяем попадание if(RaySphereIntTest(&ray, &BSphere)) ::MessageBox(0, "Hit!", "HIT", 0);
break;
Пересечение луча и объекта
Поместив луч выбора и объекты в одну систему координат, мы готовы проверить какие объекты пересекает луч. Поскольку объекты представлены сетками с треугольными ячейками, один из возможных способов заключается в следующем. Для каждого объекта мы перебираем элементы его списка граней и проверяем не пересекает ли луч какой-нибудь из этих треугольников. Если да, значит луч попал в тот объект, которому принадлежит треугольник.
Однако, выполнение проверки пересечения с лучом для каждого треугольника сцены требует много времени на вычисления. Более быстрый, хотя и менее точный метод— представить каждый объект с помощью ограничивающей сферы. Тогда мы выполняем проверку пересечения луча и ограничивающей сферы и тот объект, чью ограничивающую сферу пересекает луч, считается выбранным.
ПРИМЕЧАНИЕ
Зная центральную точку c и радиус r сферы, мы можем проверить находится ли точка p на поверхности сферы с помощью следующей простой формулы:
Пользователь выбирает чайник
Рисунок 15.1. Пользователь выбирает чайник

Мы знаем о чайнике то, что его изображение было спроецировано на область экрана внутри которой находится точка s. Более правильно будет сказать, что чайник споецирован в окне проекции таким образом, что точка окна проекции p, соответствующая точке экрана s находится внутри занимаемой им области. Так как эта задача зависит от связи между объектом и его проекцией, решение нам поможет найти Рисунок 15.2.
Преобразование из экранного пространства в окно проекции
Самой первой задачей является преобразование точки на экране в координатную систему окна проекции. Матрица преобразования порта просмотра выглядит так:
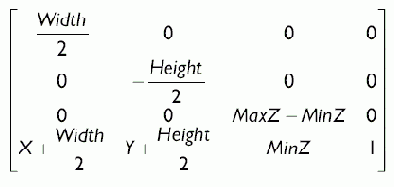
Применение данного преобразования к точке окна проекции p = (px, py, pz) дает точку экрана s = (sx, sy):

Обратите внимание, что после преобразования порта просмотра координата Z точки не сохраняется как часть двухмерного изображения, а переносится в буфер глубины.
В нашей ситуации нам известна точка экрана s, а мы должны найти точку p. Решая приведенные уравнения мы получаем:
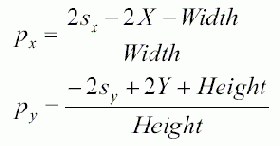
Предполагая, что значения X и Y для порта просмотра равны 0, как обычно и бывает, мы можем упростить формулы и получим:

По определению окно проекции совпадает с плоскостью z = 1; поэтому pz = 1.
Но это еще не все. Матрица проекции масштабирует точки окна проекции, чтобы имитировать различные углы поля зрения. Чтобы получить параметры точки до масштабирования, мы должны инвертировать операцию масштабирования. Для матрицы проекции P коэффициенты масштабирования точки по осям X и Y это элементы P00 и P11, так что мы получаем формулы:

Преобразование лучей
Луч выбора, который мы вычислили в предыдущем разделе, описан в пространстве вида. Чтобы выполнить проверку пересечения луча и объекта необходимо, чтобы и луч и объект находились в одной и той же системе координат. Вместо того, чтобы преобразовывать все объекты в пространстве вида, зачастую проще преобразовать луч выбора в мировое пространство или даже в локальное пространство объекта.
Мы можем преобразовать луч r(t) = p0 + tu преобразовав его начальную точку p0 и вектор направления u путем умножения на матрицу преобразования. Обратите внимание, что начальная точка преобразуется как точка, а направление обрабатывается как вектор. В рассматриваемом в данной главе примере программы для преобразования лучей реализована следующая функция:
void TransformRay(d3d::Ray* ray, D3DXMATRIX* T) { // Преобразование начальной точки луча, w = 1. D3DXVec3TransformCoord( &ray->_origin, &ray->_origin, T);
// Преобразование вектора направления луча, w = 0. D3DXVec3TransformNormal( &ray->_direction, &ray->_direction, T);
// Нормализация вектора направления D3DXVec3Normalize(&ray->_direction, &ray->_direction); }
Функции D3DXVec3TransformCoord и D3DXVec3TransformNormal получают в качестве параметра трехмерный вектор, но обратите внимание, что функция D3DXVec3TransformCoord подразумевает что четвертая компонента вектора w = 1. В противоположность ей функция D3DXVec3TransformNormal подразумевает, что четвертая компонента вектора w = 0. Следовательно, мы используем D3DXVec3TransformCoord для преобразования точек, а D3DXVec3TransformNormal — для преобразования векторов.
Вычисление луча выбора
Вспомните, что луч описывается параметрическим уравнением p(t) = p0 + tu, где p0 — это точка, являющаяся началом луча, а u — это вектор, задающий направление луча.
На Рисунок 15.2 видно, что начало луча является также началом координат пространства вида, так что p0 = (0, 0, 0). Если p — это точка окна проекции, через которую проходит луч, то вектор направления u получаем по формуле u = p – p0 = (px, py, 1) – (0, 0, 0) = p.
Приведенный ниже метод вычисляет луч выбора в пространстве вида по заданным координатам x и y точки экранного пространства, по которой был выполнен щелчок:
d3d::Ray CalcPickingRay(int x, int y) { float px = 0.0f; float py = 0.0f;
D3DVIEWPORT9 vp; Device->GetViewport(&vp);
D3DXMATRIX proj; Device->GetTransform(D3DTS_PROJECTION, &proj);
px = ((( 2.0f*x) / vp.Width) - 1.0f) / proj(0, 0); py = (((-2.0f*y) / vp.Height) + 1.0f) / proj(1, 1);
d3d::Ray ray; ray._origin = D3DXVECTOR3(0.0f, 0.0f, 0.0f); ray._direction = D3DXVECTOR3(px, py, 1.0f);
return ray; }
где определение Ray выглядит так:
struct Ray { D3DXVECTOR3 _origin; D3DXVECTOR3 _direction; };
Мы обновляем файл d3dUtility.h и пространство имен d3d, добавляя туда определение Ray.
