Часть IIIПрименение Direct
В этой части мы сосредоточимся на применении Direct3D для реализации ряда трехмерных приложений, демонстрирующих такие техники как визуализация ландшафтов, системы частиц, выбор объектов и создание гибкого класса трехмерной камеры. Кроме того, мы посвятим некоторое время продолжению изучения библиотеки D3DX (в частности, тем ее частям, которые относятся к работе с сетками). Вот краткий обзор составляющих эту часть глав.
Глава 9, «Шрифты» — Во время игры часто требуется отобразить предназначенную для пользователя текстовую информацию. В этой главе мы обсудим три способа вывода текста, поддерживаемых Direct3D.
Глава 10, «Сетки: часть I» — Эта глава посвящена детальному исследованию членов данных и методов интерфейса сеток ID3DXMesh из библиотеки D3DX.
Глава 11, «Сетки: часть II» — В этой главе мы продолжим изучение относящихся к сеткам интерфейсов и функций библиотеки D3DX. Мы узнаем о файлах .X и о том, как загружать и визуализировать их. Кроме того, мы изучим интерфейс прогрессивных сеток ID3DXPMesh. В главе также будет рассказано о том, как вычислить ограничивающий прямоугольник и ограничивающую сферу для сетки.
Глава 12, «Построение гибкого класса камеры» — В этой главе мы разработаем и реализуем гибкий класс камеры с шестью степенями свободы. Такая камера может использоваться в авиационных имитаторах и играх с видом от первого лица.
Глава 13, «Основы визуализации ландшафтов» — Глава показывает как создать, текстурировать, осветить и визуализировать трехмерный ландшафт. Помимо этого мы покажем как можно плавно перемещать камеру, чтобы создавалось впечатление ходьбы по созданному ландшафту.
Глава 14, «Системы частиц» — В этой главе мы узнаем о том, как моделировать системы, состоящие из большого количества мелких частиц, которые ведут себя одинаковым образом. Системы частиц могут использоваться, например, для моделирования падающих снега и дождя, вспышек взрывов, клубов дыма, следов от ракет и даже пуль.
Глава 15, «Выбор объектов» — Эта глава посвящена описанию алгоритма, позволяющего определить, какой именно трехмерный объект сцены выбрал пользователь с помощью мыши. Выбор объектов необходим для трехмерных игр и приложений в которых пользователь взаимодействует с трехмерным виртуальным окружением с помощью мыши.
Часть IIОсновы Direct
В этой части вы изучите основные концепции и техники Direct3D, которые будете применять в остальной части книги. Овладев этими начальными знаниями можно перейти к написанию более интересных приложений. Ниже приведен краткий обзор, входящих в эту часть книги глав.
Глава 1, «Инициализация Direct3D» — В этой главе вы узнаете что такое Direct3D и как инициализировать его, чтобы подготовиться к рисованию трехмерной графики.
Глава 2, «Конвейер визуализации» — Первой темой этой главы является изучение того, как посредством математики можно описать трехмерный мир и виртуальную камеру, представляющую собой точку из которой мы смотрим на мир. Второй темой является изучение этапов, необходимых для получения двухмерной картинки трехмерного мира, показывающей то, что «видит» камера; все эти этапы вместе называются конвейером визуализации (rendering pipeline).
Глава 3, «Рисование в Direct3D» — В данной главе мы покажем вам как рисовать трехмерные объекты в Direct3D. Вы узнаете как хранить геометрические данные в форме, пригодной для использования в Direct3D, и познакомитесь с командами рисования Direct3D. Кроме того, вы узнаете как с помощью состояний визуализации можно настраивать способ отображения объектов в Direct3D.
Глава 4, «Цвет» — В данной главе мы узнаем о том, как в Direct3D представляются цвета и как можно окрасить трехмерный графический примитив. Кроме того, мы рассмотрим два способа, какими назначенные вершинам цвета влияют на закрашивание всего примитива.
Глава 5, «Освещение» — В главе мы узнаем как создавать источники света и задавать взаимодействие световых лучей и поверхностей. Освещение добавляет сцене реализма и позволяет подчеркнуть форму и объем составляющих сцену объектов.
Глава 6, «Текстурирование» — В этой главе описывается наложение текстур (texture mapping). Это техника, используемая для увеличения реализма сцен путем наложения двухмерных изображений на трехмерные примитивы. Например, наложение текстур позволяет изобразить кирпичную стену наложив двухмерное изображение кирпичной стены на трехмерный прямоугольник.
Глава 7, «Смешивание» — В этой главе мы изучим технику, называемую смешиванием (blending). Она позволяет реализовать ряд эффектов, в частности, прозрачные объекты, которые будут выглядеть как стеклянные.
Глава 8, «Трафареты» — В этой главе рассматривается буфер трафарета, который позволяет указать, какие пикселы отображать, а какие — нет. Для иллюстрации рассматриваемых в главе идей иы рассмотрим реализацию с помощью буфера трафарета отражений и плоских теней.
Часть IМатематическая подготовка
В этой подготовительной части мы познакомим вас с математическими инструментами, которые будут применяться в остальной части книги. Главными темами обсуждения являются векторы, матрицы и преобразования, которые применяются почти в каждом приведенном в книге примере программы. Кроме того рассматриваются плоскости и лучи, поскольку некоторые программы из книги ссылаются на эти понятия; при первом чтении книги данные разделы можно пропустить.
Обсуждение ведется в легком и неформальном стиле, чтобы материал был доступен читателям с разным уровнем знаний математики. Тем, кто хочет изучить затронутые здесь темы более подробно и глубоко лучше всего обратиться к учебнику линейной алгебры. Те, кто уже изучал линейную алгебру, найдут первую часть книги очень легкой для чтения и могут использовать ее для освежения своих знаний, если такая потребность вдруг возникнет.
Кроме изучения математики, мы рассмотрим используемые для моделирования этих математических объектов классы D3DX и функции, применяемые для выполнения конкретных математических операций.
| Цели | |
|
Изучить геометрию и алгебру векторов и их применение в трехмерной компьютерной графике. Изучить матрицы, их алгебру и как они используются в трехмерной геометрии для преобразований. Изучить, как с помощью алгебры можно моделировать плоскости и лучи, и их применение в трехмерной графике. Познакомиться с используемым для выполнения операций трехмерной математики подмножеством классов и функций, предоставляемым библиотекой D3DX. |
Часть IVШейдеры и эффекты
До сих пор мы достигали желаемого эффекта путем изменения конфигурации состояний устройства таких как преобразования, освещение, текстуры и режимы визуализации. Хотя набор поддерживаемых конфигураций обеспечивает достаточную гибкость, мы ограничены предопределенными операциями (отсюда и название «фиксированный конвейер функций»).
Главная тема этой части — вершинные и пиксельные шейдеры, которые заменяют части фиксированного конвейера функций реализуемыми нами программами, которые называются шейдеры (shader). Шейдеры полностью программируемы и позволяют нам реализовать техники, которые отсутствуют в фиксированном конвейере функций. В результате количество доступных техник значительно расширяется. Программируемые части конвейера визуализации обычно называют программируемым конвейером. Ниже приведен краткий обзор глав этой части книги.
Глава 16, «Введение в высокоуровневый язык шейдеров» — В этой главе мы познакомим вас с высокоуровневым языком шейдеров (High-Level Shading Language, HLSL). Этот язык мы будем использовать в данной книге для написания программ вершинных и пиксельных шейдеров.
Глава 17, «Знакомство с вершинными шейдерами» — В этой главе мы узнаем что такое вершинные шейдеры и как их создать и использовать в Direct3D. Работа с вершинными шейдерами иллюстрируется исследованием реализации техники мультипликационного затенения.
Глава 18, «Знакомство с пиксельными шейдерами» — В этой главе мы узнаем что такое пиксельные шейдеры и как их создать и использовать в Direct3D. В качестве примера в главе будет рассмотрена реализация мультитекстурирования с использованием пиксельных шейдеров.
Глава 19, «Каркас эффектов» — В этой главе мы обсудим каркас эффектов Direct3D. В главе объясняется назначение каркаса эффектов, структуру и синтаксис файлов эффектов и создание и использование файлов эффектов в приложениях Direct3D.
DXPLANE
D3DXPLANE
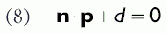
Для представления плоскости в коде достаточно указать вектор нормали n и константу d. Можно думать об этом как о четырехмерном векторе, который мы будем обозначать (n,d). В библиотеке D3DX для плоскостей используется следующая структура:
typedef struct D3DXPLANE { #ifdef __cplusplus public: D3DXPLANE() {} D3DXPLANE(CONST FLOAT*); D3DXPLANE(CONST D3DXFLOAT16*); D3DXPLANE(FLOAT a, FLOAT b, FLOAT c, FLOAT d);
// приведение типа operator FLOAT* (); operator CONST FLOAT* () const;
// унарные операторы D3DXPLANE operator + () const; D3DXPLANE operator - () const;
// бинарные операторы BOOL operator == (CONST D3DXPLANE&) const; BOOL operator != (CONST D3DXPLANE&) const; #endif //__cplusplus FLOAT a, b, c, d; } D3DXPLANE, *LPD3DXPLANE;
где a, b, и c — это компоненты вектора нормали плоскости n, а d — это константа d из формулы (8).
Единичная матрица
Единичная матрица
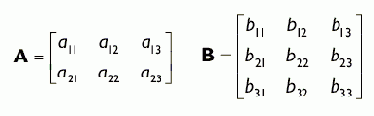
Существует особая матрица, называемая единичной матрицей (identity matrix). Это квадратная матрица все элементы которой равны нулю, за исключением тех, что расположены на главной диагонали — эти элементы равны единице. Ниже приведены примеры единичных матриц размером 2 × 2, 3 × 3 и 4 × 4:
Инвертирование матриц
Инвертирование матриц
В математике матриц нет аналога операции деления, но зато есть мультипликативная операция инвертирования. Приведенный ниже список обобщает важные особенности инвертирования:
Инвертировать можно только квадратные матрицы, так что когда мы говорим об инвертировании матрицы, подразумевается, что мы имеем дело с квадратной матрицей.
В результате инвертирования матрицы M размером n× n получается матрица размером n × n, которую мы будем обозначать M-1.
Не всякую квадратную матрицу можно инвертировать.
Если перемножить исходную и инвертированную матрицы, получится единичная матрица: MM-1 = M-1M = I. Обратите внимание, что в случае перемножения исходной и инвертированной матриц операция умножения матриц коммутативна.
Инверсия матриц применяется для нахождения искомой матрицы в уравнениях. Для примера возьмем выражение p' = pR и предположим, что нам известны p' и R, а требуется найти p. Сначала вычислим R-1 (подразумевается, что эта матрица существует). Получив R-1 можно вычислить p по следующему алгоритму:
Векторы используются для моделирования физических
Векторы используются для моделирования физических величин, которые характеризуются величиной и направлением. Геометрическим представлением вектора является направленный отрезок прямой. Когда вектор находится в стандартной позиции его начало совпадает с началом координат. Вектор в стандартной позиции описывается путем указания координат конца вектора.
Мы можем использовать матрицы 4 × 4 для представления преобразований и однородные векторы 1 × 4 для описания точек и векторов. В результате умножения вектора-строки 1 × 4 на матрицу преобразования 4 × 4 получается новый преобразованный вектор-строка 1 × 4. Можно скомбинировать несколько матриц преобразований в одну перемножив их друг на друга.
Для представления векторов и точек мы используем однородные четырехмерные векторы. Для вектора значение компоненты w равно 0, а для точки значение компоненты w равно 1. Если w ≠ 0 и w ≠ 1, то у нас есть вектор (x, y, z, w) в однородном пространстве, который может быть отображен обратно на трехмерное пространство путем деления каждой его компоненты на w;
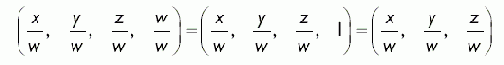
Плоскости делят трехмерное пространство на две части: положительное полупространство перед плоскостью и отрицательное полупространство за ней. Плоскости применяются для проверки местоположения точек относительно них (другими словами, чтобы проверить в каком полупространстве относительно данной плоскости находится точка).
Лучи описываются путем указания начальной точки и вектора направления. Лучи полезны для моделирования различных физических явлений, таких как луч света или полет снаряда (например, пули или ракеты) по прямолинейной траектории.
Комбинирование преобразований
Комбинирование преобразований

Часто мы будем применять к векторам целую последовательность преобразований. Например, мы можем масштабировать вектор, затем повернуть его и потом переместить в требуемую позицию.
В качестве примера мы рассмотрим вектор p= [5, 0, 0, 1], который масштабируем по всем осям с коэффициентом 1/5, затем повернем его на π/4 радиан вокруг оси Y и, наконец, переместим на 1 единицу по оси X, 2 единицы по оси Y и –3 единицы по оси Z.
Обратите внимание, что мы должны выполнить масштабирование, поворот вокруг оси Y и перемещение. Мы инициализируем наши матрицы преобразований S, Ry, T для масштабирования, поворота и перемещения соответственно, следующим образом:
Лучи
Предположим, что в разрабатываемой нами игре игрок стреляет из ружья в противника. Как определить попала ли в цель пуля, выпущенная из заданной точки в указанном направлении? Один из возможных подходов: моделирование траектории пули с помощью луча и моделирование врага с помощью ограничивающей сферы (bounding sphere). (Ограничивающая сфера— это просто сфера минимального диаметра, в которую помещается весь объект целиком, что позволяет приблизительно представить занимаемый им объем. Более подробно об ограничивающих сферах мы поговорим в главе 11.) Тогда с помощью математических вычислений мы можем определить пересекает ли луч сферу и, если да, то где. В данном разделе мы обсудим математическую модель лучей.
Лучи
Луч описывается путем указания начальной точки и направления. Параметрическая формула луча выглядит следующим образом:
Матрицы
В этом разделе мы сосредоточимся на математике матриц. Их использование в трехмерной компьютерной графике будет рассмотрено в следующем разделе.
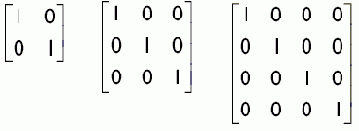
Матрицей m× n называется прямоугольный массив чисел, состоящий из m строк и n столбцов. Количество строк и столбцов определяет размер матрицы. Отдельный элемент матрицы идентифицируется путем указания его строки и столбца в состоящем из двух элементов спсике индексов; первый индекс определяет строку, а второй — столбец. Ниже в качестве примера приведены матрицы M размером 3 × 3, В размером 2 × 4 и С размером 3 × 2:
Матрицы в библиотеке DX
Матрицы в библиотеке D3DX

Программируя приложения Direct3D мы чаще всего будем использовать матрицы 4 × 4 и векторы-строки 1 × 4. Обратите внимание, что использование матриц двух указанных размеров подразумевает, что определены результаты следующих операций умножения матриц:
Умножение вектора-строки на матрицу. То есть, если v — это вектор-строка 1 × 4, а T — это матрица 4 × 4, произведение vT определено и представляет собой вектор-строку 1 × 4.
Умножение матрицы на матрицу. То есть, если T — это матрица 4 × 4 и R — это матрица 4 × 4, произведения TR и RT определены и оба являются матрицами 4 × 4. Обратите внимание, что произведение TR не обязательно равно RT, поскольку операция умножения матриц не коммутативна.
Для представления вектора-строки 1 × 4 в библиотеке D3DX, мы будем использовать классы векторов D3DXVECTOR3 и D3DXVECTOR4. Конечно, в классе D3DXVECTOR3 только три компоненты, а не четыре. Однако обычно подразумевается что четвертая компонента равна нулю или единице (более подробно это будет обсуждаться в следующем разделе).
Для представления матриц 4 × 4 в библиотеке D3DX, мы используем класс D3DXMATRIX, определение которого выглядит следующим образом:
typedef struct D3DXMATRIX : public D3DMATRIX { public: D3DXMATRIX() {}; D3DXMATRIX(CONST FLOAT*); D3DXMATRIX(CONST D3DMATRIX&); D3DXMATRIX(FLOAT _11, FLOAT _12, FLOAT _13, FLOAT _14, FLOAT _21, FLOAT _22, FLOAT _23, FLOAT _24, FLOAT _31, FLOAT _32, FLOAT _33, FLOAT _34, FLOAT _41, FLOAT _42, FLOAT _43, FLOAT _44);
// получение элемента FLOAT& operator () (UINT Row, UINT Col); FLOAT operator () (UINT Row, UINT Col) const;
// приведение типа operator FLOAT* (); operator CONST FLOAT* () const;
// операторы присваивания D3DXMATRIX& operator *= (CONST D3DXMATRIX&); D3DXMATRIX& operator += (CONST D3DXMATRIX&); D3DXMATRIX& operator -= (CONST D3DXMATRIX&); D3DXMATRIX& operator *= (FLOAT); D3DXMATRIX& operator /= (FLOAT);
// унарные операторы D3DXMATRIX operator + () const; D3DXMATRIX operator - () const;
// бинарные операторы D3DXMATRIX operator * (CONST D3DXMATRIX&) const; D3DXMATRIX operator + (CONST D3DXMATRIX&) const; D3DXMATRIX operator - (CONST D3DXMATRIX&) const; D3DXMATRIX operator * (FLOAT) const; D3DXMATRIX operator / (FLOAT) const;
friend D3DXMATRIX operator * (FLOAT, CONST D3DXMATRIX&);
BOOL operator == (CONST D3DXMATRIX&) const; BOOL operator != (CONST D3DXMATRIX&) const; } D3DXMATRIX, *LPD3DXMATRIX;
Класс D3DXMATRIX наследует элементы данных от простой структуры D3DMATRIX, определенной следующим образом:
typedef struct _D3DMATRIX { union { struct { float _11, _12, _13, _14; float _21, _22, _23, _24; float _31, _32, _33, _34; float _41, _42, _43, _44; }; float m[4][4]; }; } D3DMATRIX;
Обратите внимание, что в классе D3DXMATRIX есть десятки полезных операторов для проверки равенства, сложения и вычитания матриц, умножения матрицы на скаляр, преобразования типов и — самое главное — перемножения двух объектов типа D3DXMATRIX. Поскольку умножение матриц так важно, приведем пример кода, использующего этот оператор:
D3DXMATRIX A(Е); // инициализация A D3DXMATRIX B(Е); // инициализация B D3DXMATRIX C = A * B; // C = AB
Другим важным оператором класса D3DXMATRIX являются скобки, позволяющие легко получить доступ к отдельным элементам матрицы. Обратите внимание, что при использовании скобок нумерация элементов матрицы начинается с нуля, подобно нумерации элементов массива в языке С. Например, чтобы обратиться к верхнему левому элементу матрицы, следует написать:
D3DXMATRIX M; M(0, 0) = 5.0f; // Присвоить первому элементу матрицы значение 5.0f.
Кроме того, библиотека D3DX предоставляет набор полезных функций, позволяющих инициализировать единичную матрицу D3DXMATRIX, транспонировать матрицу D3DXMATRIX и инвертировать матрицу D3DXMATRIX:
D3DXMATRIX *D3DXMatrixIdentity( D3DXMATRIX *pout // Матрица, инициализируемая как единичная );
D3DXMATRIX M; D3DXMatrixIdentity(&M); // M = единичная матрица
D3DXMATRIX *D3DXMatrixTranspose( D3DXMATRIX *pOut, // Результат транспонирования матрицы CONST D3DXMATRIX *pM // Транспонируемая матрица );
D3DXMATRIX A(...); // инициализация A D3DXMATRIX B; D3DXMatrixTranspose(&B, &A); // B = транспонированная(A)
D3DXMATRIX *D3DXMatrixInverse( D3DXMATRIX *pOut, // возвращает результат инвертирования pM FLOAT *pDeterminant, // детерминант, если необходим, иначе 0 CONST D3DXMATRIX *pM // инвертируемая матрица );
Функция инвертирования возвращает NULL, если переданная ей матрица не может быть инвертирована. Кроме того, в этой книге мы игнорируем второй параметр и всегда передаем в нем 0.
D3DXMATRIX A(...); // инициализация A D3DXMATRIX B; D3DXMatrixInverse(&B, 0, &A); // B = инвертированная(A)
Некоторые функции для преобразования векторов
Некоторые функции для преобразования векторов

Библиотека D3DX предоставляет две функции для преобразования точек и векторов соответственно. Функция D3DXVec3TransformCoord используется для преобразования точек и предполагает, что четвертая компонента вектора равна 1. Функция D3DXVec3TransformNormal используется для преобразования векторов и предполагает, что четвертая компонента вектора равна 0.
D3DXVECTOR3 *D3DXVec3TransformCoord( D3DXVECTOR3* pOut, // Результат CONST D3DXVECTOR3* pV, // Преобразуемая точка CONST D3DXMATRIX* pM // Матрица преобразования );
D3DXMATRIX T(...); // инициализация матрицы преобразований D3DXVECTOR3 p(...); // инициализация точки D3DXVec3TransformCoord(&p, &p, &T); // преобразование точки
D3DXVECTOR3 *D3DXVec3TransformNormal( D3DXVECTOR3 *pOut, // Результат CONST D3DXVECTOR3 *pV, // Преобразуемый вектор CONST D3DXMATRIX *pM // Матрица преобразования );
D3DXMATRIX T(...); // инициализация матрицы преобразований D3DXVECTOR3 v(...); // инициализация вектора D3DXVec3TransformNormal(&v, &v, &T); // преобразование вектора
ПРИМЕЧАНИЕ
Библиотека D3DX также предоставляет функции D3DXVec3TransformCoordArray и D3DXVec3TransformNormalArray для преобразования массива точек и массива векторов соответственно.Нормализация плоскости
Нормализация плоскости
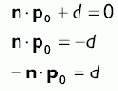
Иногда может сложиться такая ситуация, что у нас есть плоскость и нам надо нормализовать ее вектор нормали. На первый взгляд нам достаточно нормализовать вектор нормали как любой другой вектор. Но вспомните, что в формуле nЧ p + d = 0 d = –n Ч p0. Как видите, длина вектора нормали влияет на константу d. Следовательно, если мы нормализуем вектор нормали, нам надо заново вычислить d. Обратите внимание, что
Нормализация вектора
Нормализация вектора
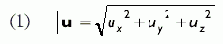
В результате нормализации получается вектор, направление которого совпадает с исходным, а модуль равен единице (единичный вектор). Чтобы нормализовать произвольный вектор, достаточно разделить каждый компонент вектора на модуль вектора, как показано ниже:
Основные преобразования
Создавая использующие Direct3D программы, для представления преобразований мы будем применять матрицы 4× 4. Идея заключается в следующем: мы инициализируем элементы матрицы X размером 4 × 4 таким образом, чтобы они описывали требуемое преобразование. Затем мы помещаем координаты точки или компоненты вектора в столбцы вектора-строки v размером 1 × 4. Результатом произведения vX будет новый преобразованный вектор v'. Например, если матрица X представляет перемещение на 10 единиц вдоль оси X, и v = [2, 6, –3, 1], произведение vX = v' = [12, 6, –3, 1].
Следует пояснить несколько моментов. Мы используем матрицы размера 4 × 4 по той причине, что они позволяют представить все необходимые нам преобразования. На первый взгляд матрицы размером 3 × 3 кажутся более подходящими для трехмерной графики. Однако, с их помощью нельзя представить ряд преобразований, которые могут нам потребоваться, таких как перемещение, перспективная проекция и отражение. Помните, что мы работаем с произведением вектора на матрицу и при выполнении преобразований ограничены правилами умножения матриц. Дополнение матрицы до размера 4 × 4 позволяет нам с помощью матрицы описать большинство преобразований и при этом произведение вектора на матрицу будет определено.
Мы упомянули, что координаты точки или компоненты вектора будем хранить в столбцах вектора-строки размером 1 × 4. Но наши точки и векторы — трехмерные! Зачем же использовать вектор-строку 1 × 4? Мы должны дополнить наши трехмерные точки/векторы до четырехмерного вектора-строки 1 × 4 чтобы был определен результат умножения вектора на матрицу; произведение вектора-строки 1 × 3 и матрицы 4 × 4 не определено.
Так какое же значение использовать для четвертой компоненты, которую, кстати, мы будем обозначать w? Когда вектор-строка 1 × 4 используется для представления точки, значение w будет равно 1.
Это позволяет корректно выполнять перемещение точки. Поскольку вектор не зависит от местоположения, операция перемещения векторов не определена и результат попытки переместить вектор не имеет смысла. Чтобы предотвратить перемещение векторов мы, помещая компоненты вектора в вектор-строку 1 × 4, присваиваем компоненте w значение 0. Например, точка p = (p1, p2, p3), помещенная в вектор-строку 1 × 4 будет выглядеть как [p1, p2, p3, 1], а вектор v = (v1, v2, v3), помещенный в вектор-строку 1 × 4 будет выглядеть как [v1, v2, v3, 0].
ПРИМЕЧАНИЕ
Мы устанавливаем w = 1 чтобы корректно осуществлялось перемещение точек. Мы устанавливаем w = 0, чтобы предотвратить перемещение векторов. Это станет более ясно, когда мы рассмотрим реальную матрицу переноса.
ПРИМЕЧАНИЕ
Дополненный четырехмерный вектор называется однородным вектором (homogenous vector) и, поскольку однородный вектор может описывать и точки и векторы, мы будем использовать термин «вектор», подразумевая, что он может относиться как к точке, так и к вектору.
Иногда в результате преобразований компонента w вектора будет меняться таким образом, что w ≠ 0 и w ≠ 1. Взгляните на следующий пример:
Пересечение луча и плоскости
Пересечение луча и плоскости
Предположим, у нас есть луч p(t) = p0 + tu и плоскость n Ч p + d = 0, и мы хотим определить пересекает ли луч плоскость и, если да, то вычислить координаты точки пересечения. Для этого мы помещаем формулу луча в формулу плоскости и вычисляем такое значение параметра t, которое удовлетворяет уравнению плоскости. Подстановка найденного значения в уравнение луча позволяет вычислить координаты точки пересечения.
Подставляем формулу (9) в формулу плоскости:
 |
Подставляем уравнение луча в формулу плоскости. | |
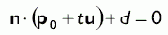 |
||
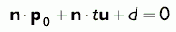 |
Раскрываем скобки. | |
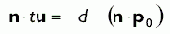 |
||
 |
Выносим за скобки переменную. | |
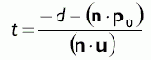 |
Решение для t. |
Если значение t не находится в диапазоне [0, ∞), значит луч не пересекает плоскость.
Если значение t находится в диапазоне [0, ∞), точка пересечения находится путем подстановки найденного значения параметра в формулу луча:
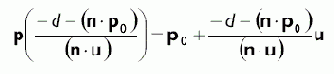
Плоскости
Плоскость описывается с помощью вектора n и принадлежащей плоскости точки p0. Вектор n называется вектором нормали (normal vector) плоскости и должен быть перпендикулярен плоскости (Рисунок 11).
j перпендикулярен как вектору k,
Решение

Таким образом, j = (0, 1, 0). Вспомните, в предыдущем разделе «Скалярное произведение векторов» говорилось, что если u Ч v = 0, значит u ^ v. Поскольку j Ч k = 0 и j Ч i = 0, мы знаем что вектор j перпендикулярен как вектору k, так и вектору i.
Преобразование плоскости
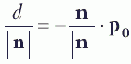 Ленджел в своей книге «Mathematics for 3D Game Programming & Computer Graphics» показал, что мы можем преобразовать плоскость ( Равенство, умножение матрицы на скаляр и сложение матриц
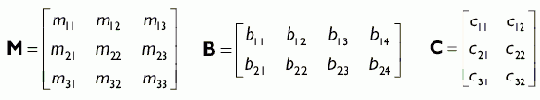 Для пояснения рассматриваемых терминов в данном разделе будут использованые следующие четыре матрицы: Равенство векторов
В геометрии два вектора считаются равными, если они указывают в одном и том же направлении и имеют одинаковую длину. В алгебре говорят, что векторы равны, если у них одинаковое количество измерений и их соответствующие компоненты равны. Например, (ux,uy, uz) = (vx, vy, vz) если ux = vx, uy = vy и uz = vz. В коде мы можем проверить равны ли два вектора, используя перегруженный оператор равенства: D3DXVECTOR u(1.0f, 0.0f, 1.0f); D3DXVECTOR v(0.0f, 1.0f, 0.0f); if( u == v ) return true; Аналогичным образом, можно убедиться, что два вектора не равны, используя перегруженный оператор неравенства: if( u != v ) return true; ПРИМЕЧАНИЕ | Сравнивая числа с плавающей точкой следует быть очень аккуратным, поскольку из-за погрешностей округления, два числа с плавающей точкой, которые должны быть равными, могут слегка отличаться. По этой причине мы проверяем приблизительное равенство чисел с плавающей точкой. Для этого мы определили константу EPSILON, содержащую очень маленькое значение, которое будет служить «буфером». Мы будем говорить, что два числа приблизительно равны, если разница между ними меньше EPSILON. Другими словами, EPSILON дает нам некий допуск для ошибок округления чисел с плавающей точкой. Приведенная ниже функция показывает, как EPSILON может использоваться при проверке равенства двух чисел с плавающей точкой:
const float EPSILON = 0.001f; bool Equals(float lhs, float rhs) { // если lhs == rhs разность должна быть равна нулю return fabs(lhs - rhs) < EPSILON ? true : false; } Об этом не надо беспокоиться, работая с классом D3DXVECTOR, поскольку перегруженные операции сравнения все сделают за нас, но очень важно знать об этой особенности сравнения чисел с плавающей точкой. |
|
br>
Для вычисления векторного произведения двух векторов в библиотеке D3DX предназначена следующая функция:
D3DXVECTOR3 *D3DXVec3Cross( D3DXVECTOR3* pOut, // Результат CONST D3DXVECTOR3* pV1, // Левый операнд CONST D3DXVECTOR3* pV2 // Правый операнд );
Как явствует из Рисунок 7, вектор –p также взаимно перпендикулярен векторам u и v. Какой из векторов, p или –p будет возвращен в качестве результата векторного произведения определяется порядком операндов. Другими словами, u × v = –(v × u). Это заначит, что операция векторного произведения не является коммутативной. Определить, какой вектор будет возвращен в качестве результата, можно с помощью правила левой руки. (Мы используем правило левой руки, поскольку работаем с левосторонней системой координат. Если бы у нас была правосторонняя система координат, пришлось бы воспользоваться правилом правой руки.) Если расположить пальцы левой руки вдоль первого вектора, а ладонь руки — вдоль второго, отогнутый на 90 градусов большой палец укажет направление результирующего вектора.
1 Теорема косинусов определяет зависимость между сторонами и углами треугольника. Она утверждает, что во всяком треугольнике квадрат длины стороны равен сумме квадратов двух других сторон без удвоенного произведения длин этих сторон на косинус угла между ними. Если угол прямой, то теорема косинусов переходит в теорему Пифагора, т.к. косинус прямого угла равен 0.
Рисунок Если точка pпринадлежит
Рисунок 12. Если точка p0 принадлежит плоскости, то точка p также принадлежит этой плоскости в том случае, если вектор (p – p0) перпендикулярен вектору нормали плоскости
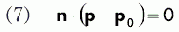
При описании конкретной плоскости вектор нормали n и принадлежащая плоскости точка p0 обычно фиксированы, и формула (7) записывается в следующем виде:
Рисунок Луч, заданный начальной
Рисунок 14. Луч, заданный начальной точкой p0 и вектором направления u. Мы можем генерировать точки луча, подставляя в формулу различные значения t, которые должны быть больше или равны нулю
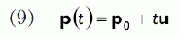
В формуле луча p0 — это начальная точка, u — это вектор, задающий направление луча, а t — это параметр. Подставляя различные значения t, мы сможем получать координаты различных точек луча. Причем для луча значение t должно находиться в диапазоне [0, ∞). Значения меньше нуля приведут к вычислению координат точек, находящихся за лучом (на прямой, частью которой является луч). Фактически, если t принимает значения из диапазона (–∞, ∞), мы получаем линию в трехмерном пространстве.
Рисунок Масштабирование с коэффициентом по оси X и коэффициентом по оси Y
Рисунок 10. Масштабирование с коэффициентом 1/2 по оси X и коэффициентом 2 по оси Y
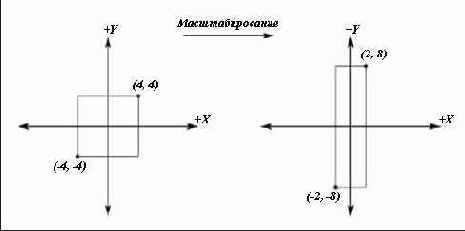
Мы можем масштабировать вектор с коэффициентом qx по оси Х, коэффициентом qy по оси Y и коэффициентом qz по оси Z, умножив его на следующую матрицу:
Рисунок Нулевой вектор и базовые орты трехмерной системы координат
Рисунок 4. Нулевой вектор и базовые орты трехмерной системы координат
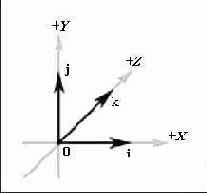
ПРИМЕЧАНИЕ
Вектор, длина которого равна единице, называется единичным вектором или ортом.В библиотеке D3DX для представления векторов в трехмерном пространстве мы можем воспользоваться классом D3DXVECTOR3. Его определение выглядит следующим образом:
typedef struct D3DXVECTOR3 : public D3DVECTOR { public: D3DXVECTOR3() {}; D3DXVECTOR3( CONST FLOAT * ); D3DXVECTOR3( CONST D3DVECTOR& ); D3DXVECTOR3( FLOAT x, FLOAT y, FLOAT z );
// приведение типа operator FLOAT* (); operator CONST FLOAT* () const;
// операторы присваивания D3DXVECTOR3& operator += ( CONST D3DXVECTOR3& ); D3DXVECTOR3& operator -= ( CONST D3DXVECTOR3& ); D3DXVECTOR3& operator *= ( FLOAT ); D3DXVECTOR3& operator /= ( FLOAT );
// унарные операторы D3DXVECTOR3 operator + () const; D3DXVECTOR3 operator - () const;
// бинарные операторы D3DXVECTOR3 operator + ( CONST D3DXVECTOR3& ) const; D3DXVECTOR3 operator - ( CONST D3DXVECTOR3& ) const; D3DXVECTOR3 operator * ( FLOAT ) const; D3DXVECTOR3 operator / ( FLOAT ) const; friend D3DXVECTOR3 operator * ( FLOAT, CONST struct D3DXVECTOR3& ); BOOL operator == ( CONST D3DXVECTOR3& ) const; BOOL operator != ( CONST D3DXVECTOR3& ) const; } D3DXVECTOR3, *LPD3DXVECTOR3;
Обратите внимание, что D3DXVECTOR3 наследует компоненты от D3DVECTOR, определение которого выглядит следующим образом:
typedef struct _D3DVECTOR { float x; float y; float z; } D3DVECTOR;
Так же, как и у скалярных величин, у векторов есть собственная арифметика, что видно из наличия описаний математических операций в определении класса D3DXVECTOR3. Возможно, сейчас вы не знаете, что делают эти методы. В следующих подразделах мы рассмотрим эти операции с векторами, другие вспомогательные функции работы с векторами из библиотеки D3DX и некоторые важные особенности обработки векторов.
ПРИМЕЧАНИЕ
Хотя основной интерес для нас представляют векторы в трехмерном пространстве, занимаясь программированием трехмерной графики мы будем иногда сталкиваться с векторами в двухмерном и четырехмерном пространствах. Библиотека D3DX предоставляет классы D3DXVECTOR2 и D3DXVECTOR4, предназначенные для представления векторов в двухмерном и четырехмерном пространствах соответственно. Векторы в пространствах с другим количеством измерений обладают теми же свойствами, что и векторы в трехмерном пространстве, а именно — длиной и направлением, отличается только количество измерений. Кроме того, математические операции с векторами, за исключением векторного произведения (см. раздел «Векторное произведение», далее в этой главе), которое определено только для трехмерной системы координат, могут быть обобщены для векторов любой размерности. Таким образом, за исключением векторного произведения, все операции, которые мы обсуждаем для векторов в трехмерном пространстве, распространяются и на векторы в двухмерном, четырехмерном и даже n-мерном пространствах.Рисунок Перемещение на единиц по оси X и на – единиц по оси Y
Рисунок 8. Перемещение на 12 единиц по оси X и на –10 единиц по оси Y
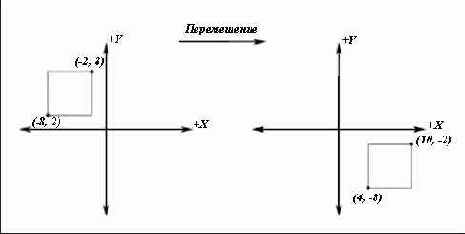
Мы можем переместить вектор (x, y, z, 1) на px единиц по оси Х, py единиц по оси Y и pz единиц по оси Z умножив его на следующую матрицу:
мы видим, что графическим
Рисунок 11. Плоскость, заданная вектором нормали n и точкой плоскости p0

Рисунок Поворот на градусов против часовой стрелки вокруг оси Z
Рисунок 9. Поворот на 30 градусов против часовой стрелки вокруг оси Z

Используя приведенные ниже матрицы мы можем повернуть вектор на φ радиан вокруг осей X, Y или Z. Обратите внимание, что если смотреть вдоль оси вращения по направлению к началу координат, то углы измеряются по часовой стрелке.
Рисунок Слева изображена левосторонняя
Рисунок 2. Слева изображена левосторонняя система координат. Обратите внимание, что положительное направление оси Z направлено вглубь страницы. Справа изображена правостороняя система координат. Здесь положительное направление оси Z направлено от страницы

Поскольку местоположение вектора не изменяет его свойств, мы можем перенести векторы таким образом, чтобы начало каждого из них совпадало с началом координат выбранной координатной системы. Когда начало вектора совпадает с началом координат, говорят, что вектор находится в стандартной позиции. Таким образом, если вектор находится в стандартной позиции, мы можем описать его, указав только координаты конечной точки. Мы будем называть эти координаты компонентами вектора. На Рисунок 3 показаны векторы, изображенные на Рисунок 1, которые были перемещены в стандартные позиции.
Рисунок Сложение векторов Обратите
 |
В коде для сложения двух векторов мы будем применять перегруженый оператор сложения:
D3DXVECTOR3 u(2.0f, 0.0f, 1.0f); D3DXVECTOR3 v(0.0f, -1.0f, 5.0f);
// (2.0 + 0.0, 0.0 + (-1.0), 1.0 + 5.0) D3DXVECTOR3 sum = u + v; // = (2.0f, -1.0f, 6.0f)
Рисунок Свободные векторы, определенные независимо от системы координат
Рисунок 1. Свободные векторы, определенные независимо от системы координат

<
Поскольку местоположение не является характеристикой вектора, два вектора с одинаковой длиной и указывающие в одном и том же направлении считаются равными, даже если они расположены в различных местах. Обратите внимание, что два таких вектора будут параллельны друг другу. Например, на Рисунок 1 векторы u и v равны.
На Рисунок 1 видно, что обсуждние векторов может вестись без упоминания системы координат, поскольку всю значимую информацию, — длину и направление, — вектор содержит в себе. Добавление системы координат не добавляет информации в вектор; скорее можно говорить, что вектор, значения которого являются его неотъемлимой частью, просто описан относительно конкретной системы координат. И если мы изменим систему координат, мы только опишем тот же самый вектор относительно другой системы.
Отметив этот важный момент, мы перейдем к изучению того, как векторы описываются в левосторонней трехмерной декартовой системе координат. На Рисунок 2 показаны левосторонняя и правосторонняя системы координат. Различие между ними — положительное направление оси Z. В левосторонней системе координат положительное направление оси Z погружается в страницу. В правосторонней системе координат положительное направление оси Z направлено от страницы.
Рисунок Точка q плоскости (, d)
   |
На Рисунок 13 видно, что q = p + (–k

Рисунок Векторное произведение Вектор p = u × v перпендикулярен как вектору u, так и вектору v
Рисунок 7. Векторное произведение. Вектор p = u × v перпендикулярен как вектору u, так и вектору v
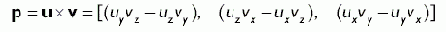
| ПРИМЕР | Вычислите j = k × i = (0, 0, 1) × (1, 0, 0) и проверьте, что вектор j перпендикулярен как вектору i, так и вектору k.
Рисунок Векторы в стандартной
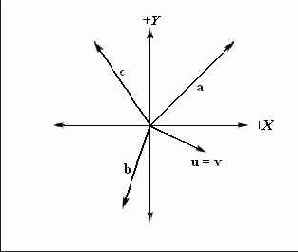 |
ПРИМЕЧАНИЕ
Поскольку мы описываем находящийся в стандартной позиции вектор, указывая его конечную точку, как если бы мы описывали отдельную точку, легко перепутать точку и вектор. Чтобы подчеркнуть различия между этими двумя понятиями, мы вновь приведем определение каждого из них. Точка описывает только местоположение в системе координат, в то время как вектор описывает величину и направление. Мы будем пользоваться для обозначения векторов полужирными строчными буквами, но иногда будем применять и полужирные заглавные буквы. Вот пример двух-, трех- и четырехмерных векторов соответственно: u= (ux, uy), N = (Nx, Ny, Nz), c = (cx, cy, cz, cw).
Теперь мы введем четыре специальных трехмерных вектора, которые показаны на Рисунок 4. Первый из них называется нулевым вектором, и значения всех его компонент равны нулю; мы будем обозначать такой вектор выделенным полужирным шрифтом нулем: 0 = (0, 0, 0). Следующие три специальных вектора называются единичными базовыми векторами (базовыми ортами) трехмерной системы координат. Эти векторы, направленные вдоль осей X, Y и Z нашей координатной системы, мы будем называть i, j и k соответственно. Модуль этих векторов равен единице, а определение выглядит следующим образом: i = (1, 0, 0), j = (0, 1, 0), k = (0, 0, 1).
Рисунок Вычитание векторов
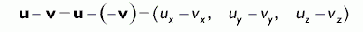 |
В коде для вычитания двух векторов мы будем применять перегруженый оператор вычитания:
D3DXVECTOR3 u(2.0f, 0.0f, 1.0f); D3DXVECTOR3 v(0.0f, -1.0f, 5.0f);
D3DXVECTOR3 difference = u - v; // = (2.0f, 1.0f, -4.0f)
Как видно на Рисунок 6, операция вычитания векторов возвращает вектор, начало которого совпадает с концом вектора v, а конец — с концом вектора u. Если мы интерпретируем компоненты u и v как координаты точек, то результатом вычитания будет вектор, направленный от одной точки к другой. Это очень удобная операция, поскольку нам часто будет необходимо найти вектор, описывающий направление от одной точки к другой.
Скалярное произведение векторов
Скалярное произведение векторов
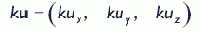
Скалярное произведение векторов— это первая из двух определенных в векторной алгебре операций умножения. Вычисляется такое произведение следующим образом:
Сложение векторов
Сложение векторов

Мы можем сложить два вектора, сложив их соответствующие компоненты; обратите внимание, что размерность складываемых векторов должна быть одинаковой:
Создание плоскостей
Создание плоскостей
Вместо непосредственного указания нормали и кратчайшего расстояния до начала координат, мы можем использовать еще два способа задания плоскостей. Зная вектор нормали n и принадлежащую плоскости точку p0 мы можем вычислить значение d следующим образом:
Точка плоскости, ближайшая к заданной
Точка плоскости, ближайшая к заданной

Пусть у нас есть точка p в трехмерном пространстве и нам необходимо найти точку q, принадлежащую плоскости (
Транспонирование матриц
Транспонирование матриц

Транспонирование матрицы осуществляется путем перестановки ее строк и столбцов. Следовательно, результатом транспонирования матрицы m × n будет матрица n × m. Результат транспонирования матрицы M мы будем обозначать MT.
ПРИМЕРТранспонируйте следующие две матрицы:
Умножение
Умножение
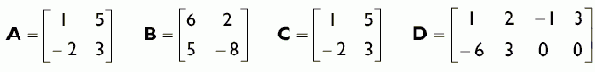
Умножение матриц это наиболее важная операция, которая постоянно используется в трехмерной компьютерной графике. Именно умножение матриц позволяет осуществлять преобразование векторов и комбинировать несколько преобразований в одно. Преобразования будут рассмотрены в следующем разделе.
Чтобы получить произведение матриц AB необходимо чтобы количество столбцов матрицы A было равно количеству строк матрицы B. Если условие выполняется, произведение матриц определено. Рассмотрим представленные ниже матрицы A и B, с размерностью 2× 3 и 3 × 3 соответственно:
Умножение вектора на скаляр
Умножение вектора на скаляр
Как видно из названия раздела, мы можем умножать вектор на скаляр, в результате чего происходит масштабирование вектора. Если масштабный множитель положителен, направление вектора не меняется. Если же множитель отрицателен, то направление вектора изменяется на противоположное (инвертируется).
Векторное произведение
Векторное произведение
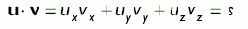
Второй формой операции умножения, определенной в векторной алгебре, является векторное произведение. В отличие от скалярного произведения, результатом которого является число, результатом векторного произведения будет вектор. Векторным произведением двух векторов u и v будет другой вектор, p, являющийся взаимно перпендикулярным для векторов u и v. Это означает, что вектор p перпендикулярен вектору u и одновременно вектор p перпендикулярен вектору v.
Вычисляется векторное произведение по следующей формуле:
Векторы в трехмерном пространстве
Геометрическим представлением вектора является направленный отрезок прямой линии, что показано на Рисунок 1. У каждого вектора есть два свойства: длина (также называемая модулем или нормой вектора) и направление. Благодаря этому векторы очень удобны для моделирования физических величин, которые характеризуются модулем и направлением. Например, в главе 14 мы реализуем систему частиц. При этом мы будем использовать векторы для моделирования скорости и ускорения наших частиц. С другой стороны, в трехмерной компьютерной графике векторы часто используются только для моделирования направления. Например, нам часто требуется указать направление распространения световых лучей, ориентацию грани или направление камеры, глядящей на трехмерный мир. Векторы обеспечивают удобный механизм задания направления в трехмерном пространстве.
Приведенная ниже функция библиотеки D3DX вычисляет значение n Ч p + d для заданных плоскости и точки:
FLOAT D3DXPlaneDotCoord( CONST D3DXPLANE *pP, // плоскость CONST D3DXVECTOR3 *pV // точка );
// Проверка местоположения точки относительно плоскости D3DXPLANE p(0.0f, 1.0f, 0.0f, 0.0f);
D3DXVECTOR3 v(3.0f, 5.0f, 2.0f);
float x = D3DXPlaneDotCoord(&p, &v);
if( x приблизительно равно 0.0f ) // v принадлежит плоскости if( x > 0 ) // v в положительном полупространстве if( x < 0 ) // v в отрицательном полупространстве
ПРИМЕЧАНИЕ
ПРИМЕЧАНИЕ
Вычисление модуля вектора
В геометрии модулем вектора называется длина направленного отрезка линии. В алгебре, зная компоненты вектора мы можем вычислить его модуль по следующей формуле: Вычитание векторов
Аналогично сложению, вычитание векторов осуществляется путем вычитания их отдельных компонент. Опять же оба вектора должны иметь одинаковую размерность. Взаимное расположение точки и плоскости
Формула (8) в основном используется для проверки местоположения точки относительно плоскости. Предположим, нам дана плоскость (n, d), и мы хотим узнать как точка p расположена относительно этой плоскости: Если n Ч p + d = 0, то точка p принадлежит плоскости. Если n Ч p + d > 0, то точка p находится перед плоскостью в положительном полупространстве плоскости. Если n Ч p + d < 0, то точка p находится за плоскостью в отрицательном полупространстве плоскости. ПРИМЕЧАНИЕ | Если длина вектора нормали плоскости n равна единице, nЧp + d — это наименьшее расстояние от плоскости до точки p. | Мы говорим «приблизительно равно», чтобы напомнить об особенностях сравнения чисел с плавающей точкой. Обратите внимание на примечание в разделе «Равенство векторов». | Существуют похожие на D3DXPlaneDotCoord методы D3DXPlaneDot и D3DXPlaneDotNormal. Их описание можно посмотреть в документации DirectX. |
